Write a bash script that prints the string "HELLO".
Input Format
There is no input file required for this problem.
Output Format
HELLO
Sample Input
-
Sample Output
HELLO
Explanation
-
SOLUTION:
echo "HELLO"
Tuesday, December 13, 2022
Morgan And A String in Java
Jack and Daniel are friends. Both of them like letters, especially uppercase ones.
They are cutting uppercase letters from newspapers, and each one of them has his collection of letters stored in a stack.
One beautiful day, Morgan visited Jack and Daniel. He saw their collections. He wondered what is the lexicographically minimal string made of those two collections. He can take a letter from a collection only when it is on the top of the stack. Morgan wants to use all of the letters in their collections.
As an example, assume Jack has collected and Daniel has . The example shows the top at index for each stack of letters. Assemble the string as follows:
Jack Daniel result
ACA BCF
CA BCF A
CA CF AB
A CF ABC
A CF ABCA
F ABCAC
ABCACF
Note the choice when there was a tie at CA and CF.
Function Description
Complete the morganAndString function in the editor below.
morganAndString has the following parameter(s):
- string a: Jack's letters, top at index
- string b: Daniel's letters, top at index
Returns
- string: the completed string
Input Format
The first line contains the an integer , the number of test cases.
The next pairs of lines are as follows:
- The first line contains string
- The second line contains string .
Constraints
- and contain upper-case letters only, ascii[A-Z].
Sample Input
2
JACK
DANIEL
ABACABA
ABACABA
Sample Output
DAJACKNIEL
AABABACABACABA
Explanation
The first letters to choose from are J and D since they are at the top of the stack. D is chosen and the options now are J and A. A is chosen. Then the two stacks have J and N, so J is chosen. The current string is DA. Continue this way to the end to get the string.
SOLUTION:
import java.io.*;
import java.util.*;
import java.text.*;
import java.math.*;
import java.util.regex.*;
public class Solution {
private static final int MAXSIZE = 200100;
private static final int ALPHABET = 128;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int testcase = Integer.parseInt(in.nextLine());
for (int i = 0; i < testcase; i++) {
String str1 = in.nextLine();
String str2 = in.nextLine();
System.out.println(solution(str1 + "a", str2 + "b"));
}
}
private static List<Integer> buildSuffixArray(String str) {
int[] p = new int[MAXSIZE];
int[] c = new int[MAXSIZE];
int[] cnt = new int[MAXSIZE];
int[] pn = new int[MAXSIZE];
int[] cn = new int[MAXSIZE];
Arrays.fill(cnt, 0);
int n = str.length();
for (int i = 0; i < n; i++) {
++cnt[str.charAt(i)];
}
for (int i = 1; i < ALPHABET; i++) {
cnt[i] += cnt[i - 1];
}
for (int i = 0; i < n; i++) {
p[--cnt[str.charAt(i)]] = i;
}
int count = 1;
c[p[0]] = count - 1;
for (int i = 1; i < n; i++) {
if (str.charAt(p[i]) != str.charAt(p[i - 1])) {
++count;
}
c[p[i]] = count - 1;
}
for (int h = 0; (1 << h) < n; ++h) {
for (int i =0; i < n; i++) {
pn[i] = p[i] - (1 << h);
if (pn[i] < 0) {
pn[i] += n;
}
}
Arrays.fill(cnt, 0);
for (int i = 0; i < n; i++) {
++cnt[c[i]];
}
for (int i = 1; i < count; i++) {
cnt[i] += cnt[i - 1];
}
for (int i = n - 1; i >= 0; i--) {
p[--cnt[c[pn[i]]]] = pn[i];
}
count = 1;
cn[p[0]] = count - 1;
for (int i = 1; i < n; i++) {
int pos1 = (p[i] + (1 << h)) % n;
int pos2 = (p[i - 1] + (1 << h)) % n;
if (c[p[i]] != c[p[i - 1]] || c[pos1] != c[pos2]) {
++count;
}
cn[p[i]] = count - 1;
}
for (int i = 0; i < n; i++) {
c[i] = cn[i];
}
}
List<Integer> res = new ArrayList<Integer>(n);
for (int i = 0; i < n; i++) {
res.add(c[i]);
}
return res;
}
private static String solution(String str1, String str2) {
StringBuilder sb = new StringBuilder(str1).append(str2);
List<Integer> suffix = buildSuffixArray(sb.toString());
StringBuilder rst = new StringBuilder();
int start1 = 0;
int start2 = 0;
while (start1 < str1.length() - 1 || start2 < str2.length() - 1) {
if (start1 >= str1.length() - 1) {
rst.append(str2.charAt(start2++));
continue;
}
if (start2 >= str2.length() - 1) {
rst.append(str1.charAt(start1++));
continue;
}
if (suffix.get(start1) < suffix.get(str1.length() + start2)) {
rst.append(str1.charAt(start1++));
} else {
rst.append(str2.charAt(start2++));
}
}
return rst.toString();
}
}
Absolute Permutation in Java
We define to be a permutation of the first natural numbers in the range . Let denote the value at position in permutation using -based indexing.
is considered to be an absolute permutation if holds true for every .
Given and , print the lexicographically smallest absolute permutation . If no absolute permutation exists, print -1.
Example
Create an array of elements from to , . Using based indexing, create a permutation where every . It can be rearranged to so that all of the absolute differences equal :
pos[i] i |pos[i] - i| 3 1 2 4 2 2 1 3 2 2 4 2
Function Description
Complete the absolutePermutation function in the editor below.
absolutePermutation has the following parameter(s):
- int n: the upper bound of natural numbers to consider, inclusive
- int k: the absolute difference between each element's value and its index
Returns
- int[n]: the lexicographically smallest permutation, or if there is none
Input Format
The first line contains an integer , the number of queries.
Each of the next lines contains space-separated integers, and .
Constraints
Sample Input
STDIN Function ----- -------- 3 t = 3 (number of queries) 2 1 n = 2, k = 1 3 0 n = 3, k = 0 3 2 n = 3, k = 2
Sample Output
2 1
1 2 3
-1
Explanation
Test Case 0:
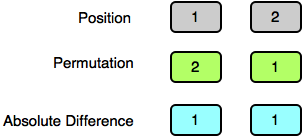
Test Case 1:
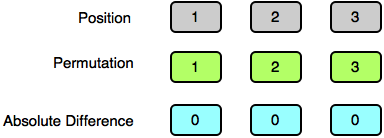
Test Case 2:
No absolute permutation exists, so we print -1 on a new line.
SOLUTION:
import java.io.*;
import java.util.*;
import java.text.*;
import java.math.*;
import java.util.regex.*;
public class Solution {
static Scanner in = new Scanner(System.in);
public static void main(String[] args) {
int t = in.nextInt();
for (int a0 = 0; a0 < t; a0++) {
int n = in.nextInt();
int k = in.nextInt();
if (k == 0) {
for (int i = 1; i <= n; i++) {
System.out.print(i + " ");
}
System.out.println();
} else if (n % 2 == 0 && n % (2 * k) == 0) {
int blocks = n / k;
int currentNumber = k;
for (int i = 0; i < blocks; i++) {
for (int j = 0; j < k; j++) {
currentNumber++;
System.out.print(currentNumber + " ");
}
if (i % 2 != 0) {
currentNumber = currentNumber + (2 * k);
} else {
currentNumber = currentNumber - (2 * k);
}
}
System.out.println();
} else {
System.out.println(-1);
}
}
}
}
Subscribe to:
Posts (Atom)
Popular Posts
-
SET NOCOUNT ON; WITH hours_worked as ( SELECT emp_id, CASE WHEN datepart(minute,TIMESTAMP) >= datepart(minute,l... -
select c.algorithm, q1.tot, q2.tot, q3.tot, q4.tot from coins c join (select sum(volume) as tot,coins.algorithm from transactions left joi... -
SELECT c.customer_name, ROUND ( SUM (i.total_price), 6 ) FROM customer c INNER JOIN invoice i ON c.id = i.customer_id GROUP BY ... -
You are updating the username policy on your company's internal networking platform. According to the policy, a username is considered...
-
The Calendar class is an abstract class that provides methods for converting between a specific instant in time and a set of calendar ...
-
Jack and Daniel are friends. Both of them like letters, especially uppercase ones. They are cutting uppercase letters from newspapers, and...
-
Write a class called MyRegex which will contain a string pattern. You need to write a regular expression and assign it to the pattern such...
-
We use the integers , , and to create the following series: You are given queries in the form of , , and . For each query, pr...
-
import math import os import random import re import sys from collections import defaultdict # # Complete the 'countPairs'... -
/*Java's System.out.printf function can be used to print formatted output. The purpose of this exercise is to test your understanding o...
